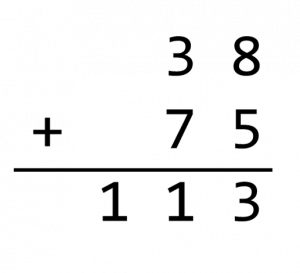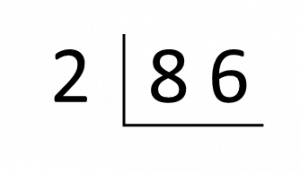청소년IT경시대회 프로그래밍 언어(파이썬) 대비: 두 판 사이의 차이
잔글편집 요약 없음 |
잔글 (→5. 비트연산자) |
||
| (같은 사용자의 중간 판 11개는 보이지 않습니다) | |||
| 1번째 줄: | 1번째 줄: | ||
== 진법 (2진법, 8진법, 16진법), 비트 연산자 == | |||
N진법 ? | |||
N진법이란 0~N-1로 각 자리를 표현해 나타내는 수 입니다. | |||
일반적으로 우리가 사용하는 숫자는 10진수입니다. 각 자리를 0~9로 나타내기 때문에 10진수이죠! | |||
0~9 의 수로 숫자를 나타내다가 더이상 표현할 수 없을 때 한 자리를 높여 다음 자리를 표현합니다. | |||
예를 들어, 38 + 75를 그림으로 알아봅시다. | |||
[[파일:38+75 1.png|테두리|프레임없음]] | |||
일의 자리를 먼저 더한 결과를 생각해보면 13입니다. 10진수는 각 자리에 0~9까지만 나타낼 수 있으므로 1을 십의 자리로 올려 계산합니다. | |||
[[파일:38+75 2.png|테두리|프레임없음]] | |||
다음 10의 자리를 계산해봅시다. 3과 8을 더한 결과는 10입니다. 일의 자리에서 올라온 1과 함께 계산하면 11입니다. 10진수는 각 자리에 0~9까지만 나타낼 수 있으므로 백의 자리로 1을 올려 계산합니다. | |||
[[파일:38+75 3.png|테두리|프레임없음]] | |||
우리가 항상 더하기 한 결과를 위와 같은 과정으로 나타내 보았습니다. | |||
=== ▶ 2진수 더하기 계산 방법 === | |||
그럼 2진수 더하기를 한 번 예시를 통해 확인해봅시다. | |||
2진수는 각 자리를 0~1로 표현할 수 있습니다. 합한 결과가 2가 되면 다음 자리로 1을 올림하여 계산하면 됩니다. | |||
예를 들어, 101 + 111를 그림으로 알아봅시다. | |||
[[파일:101 + 111 1.png|테두리|프레임없음]] | |||
먼저 10진수처럼 맨 뒤 자리부터 계산합니다. | |||
1 + 1 은 2입니다. 2진수는 각 자리를 0~1로 나타낼 수 있기 때문에 1을 다음 자리로 올려 계산합니다. | |||
[[파일:1001 + 101 3.png|테두리|프레임없음]] | |||
다음 자리를 계산해봅시다. 0과 1을 더한 값과 넘어온 1을 함께 계산하면 2입니다. 2진수는 각 자리를 0~1로 나타낼 수 있기 때문에 1을 다음 자리로 올려 계산합니다. | |||
[[파일:1001 + 101 5.png|테두리|프레임없음]] | |||
다음 자리를 계산해봅시다. 1과 1을 더한 값과 넘어온 1을 함께 계산하면 3입니다. 2진수는 각 자리를 0~1로 나타낼 수 있기 때문에 1을 다음 자리로 올려 계산합니다. | |||
[[파일:1001 + 101 6.png|테두리|프레임없음]] | |||
이진수 101 + 111 의 결과는 1100입니다. 숫자가 0과 1만 존재하는 수라고 생각해보면 쉬워요! | |||
=== ▶ 2진수 더하기 퀴즈 === | |||
아래 3개의 문제를 직접 계산해보고 선생님께 확인 받으세요. | |||
1) 1110 + 101 = ? | |||
2) 10101 + 1101 = ? | |||
3) 1011 + 1101 = ? | |||
=== 1. 2진수 === | |||
위에서 간단히 2진수에 대해서 확인해보았습니다. | |||
2진수는 0~1로 이루어진 수 입니다. | |||
2진수의 값을 나타내는 방법에 대해서 배워봅시다. | |||
먼저 너무나도 당연하게 사용하는 10진수를 생각해봅시다. | |||
[19803] 라는 수가 있다면 이 수를 나타내는 방법은 아래와 같습니다. | |||
[[파일:십진수.png|프레임없음|674x674픽셀]] | |||
10진수는 위의 표처럼 나타내고 사용합니다. | |||
'''1 X 10000 + 9 X 1000 + 8 X 100 + 0 X 10 + 3 X 1''' | |||
10진수와 2진수는 각 자리를 나타내는 수의 크기가 다를 뿐 개념은 같습니다. | |||
[101011] 라는 수는 어떻게 표현할까요? | |||
2진수를 나타내는 방법을 표로 나타내면 아래와 같습니다. | |||
[[파일:이진수.png|프레임없음|736x736픽셀]] | |||
10진수와 마찬가지로 위의 표처럼 나타내고 사용합니다. | |||
'''1 X 32 + 0 X 16 + 1 X 8 + 0 X 4 + 1 X 2 + 1 X 1''' | |||
따라서 [101011]라는 이진수를 십진수로 나타내면 위의 계산을 통해 [43]라는 것을 알 수 있습니다. | |||
=== 2. 10진수 → 2진수 변환하기 === | |||
2진수에 대해서 알아보았습니다. 그럼 10진수 N이라는 값을 2진수로 변환하는 방법을 알아봅시다. | |||
==== '''1) 2진수 변환 방법① : 2진수 자리를 이용해 채우기''' ==== | |||
위에서 배운 것을 이용해 각 자리를 생성하고 10진수의 값을 차례로 값을 넣어보면 됩니다. | |||
10진수 [86]을 2진수로 나타내봅시다. | |||
86를 2진수로 변환하기 위해서 2진수 표를 만들어봅시다. | |||
가장 큰 자리 수부터 채우면 됩니다. | |||
[[파일:2진수 변환1.png|프레임없음|867x867픽셀]] | |||
현재 만든 표에서는 가장 큰 수가 128입니다. 그러나 86은 128보다 작아서 128자리는 0으로 채우고 넘어갑니다. | |||
[[파일:2진수 변환2 .png|프레임없음|866x866픽셀]] | |||
다음은 64자리 입니다. 64자리를 1로 채웁니다. | |||
[[파일:2진수 변환3.png|프레임없음|862x862픽셀]] | |||
남은 값 [22]를 이용해 다음 자리를 계산합니다. | |||
다음 자리는 32입니다. 22는 32보다 작아서 32자리는 0으로 채우고 넘어갑니다. | |||
[[파일:2진수 변환4.png|프레임없음|864x864픽셀]] | |||
다음은 16자리 입니다. 16자리를 1로 채웁니다. | |||
[[파일:2진수 변환5.png|프레임없음|869x869픽셀]] | |||
남은 값 [6]을 이용해 다음 자리를 계산합니다. | |||
다음 자리는 8입니다. 6은 8보다 작아서 8자리는 0으로 채우고 넘어갑니다. | |||
[[파일:2진수 변환6.png|프레임없음|867x867픽셀]] | |||
다음은 4자리 입니다. 4자리를 1로 채웁니다. | |||
[[파일:2진수 변환7.png|프레임없음|865x865픽셀]] | |||
남은 값 [2]를 이용해 다음 자리를 계산합니다. | |||
2자리를 1로 채웁니다. 남은 값은 0이므로 나머지 칸을 모두 0으로 채웁니다. | |||
[[파일:2진수 변환8.png|프레임없음|863x863픽셀]] | |||
결과적으로 10진수 [86]을 2진수로 변환하면 [1010110]입니다. | |||
==== '''2) 2진수 변환 방법② : 2로 나눈 몫과 나머지를 이용해 변환하기''' ==== | |||
두 번째 방법은 10진수 값을 2로 나눈 몫과 나머지를 계산하여 2진수로 변환하는 방법입니다. | |||
이 방법이 더 쉬울 수 있어요! | |||
위의 예제처럼 [86]을 2진수로 변환하는 과정을 아래 그림으로 알아봅시다. | |||
[[파일:2진수 변환 7.png|프레임없음]] | |||
아래 그림처럼 86을 계속 2로 나눠봅시다. 몫이 1이될 때까지 몫과 나머지를 작성합니다. | |||
[[파일:2진수 변환9.png|프레임없음]] | |||
몫이 1이 되는 경우까지 작성 후 주황선을 따라 순서대로 값을 적어주면 10진수 값을 2진수로 변환한 값입니다. | |||
따라서 10진수 [86]을 2진수로 변환하면 [1010110]입니다. | |||
위에서 2진수의 자리를 채워 변환하는 방법과 같은 값이 나오는 것을 확인할 수 있습니다. | |||
==== ▶ 10진수 → 2진수 변환 퀴즈 ==== | |||
아래 3개의 문제를 직접 계산해보고 선생님께 확인 받으세요. | |||
1) 57 → ? | |||
2) 19 → ? | |||
3) 156 → ? | |||
==== ▶ 2진수 → 10진수 변환 퀴즈 ==== | |||
아래 3개의 문제를 직접 계산해보고 선생님께 확인 받으세요. | |||
1) 1000100 → ? | |||
2) 11111 → ? | |||
3) 101101 → ? | |||
=== 3. 8진수 === | |||
10진수와 2진수에 대해 공부해보았습니다. | |||
그럼 이번엔 8진수에 대해서 배워봅시다. | |||
앞에서 배웠듯 10진수는 각 자리를 0~9까지 나타낼 수 있고 2진수는 0~1까지 나타낼 수 있습니다. | |||
그러므로 8진수는 0~7까지 나타낼 수 있답니다! | |||
그럼 '''10진수를 8진수로 변환'''하는 방법을 알아봅시다. | |||
10진수를 8진수로 변환하기 위해서는 [10진수 → 2진수 → 8진수]로 단계별 과정을 거치면 쉽게 바꿀 수 있습니다. | |||
먼저 위에서 확인해보았던 10진수 [86]을 2진수로 변환하면 [1010110]입니다. 8진수는 2진수 자리를 3개씩 나눠 값을 변환하면 됩니다. | |||
[[파일:8진수.png|프레임없음|542x542픽셀]] | |||
2진수를 맨 뒷 자리부터 3개씩 나눠봅시다. | |||
맨 앞의 1은 앞에 2개의 값이 없습니다. 이때는 앞에 2개의 0이 있다고 생각해보세요. | |||
그리고 각 자리의 값을 8진수로 변환하게 되면 아래와 같습니다. | |||
[[파일:8진수2.png|프레임없음|535x535픽셀]] | |||
2진수를 8진수로 변환하면 [126]이 됩니다. | |||
==== ▶ 10진수 → 8진수 변환 퀴즈 ==== | |||
아래 3개의 문제를 직접 계산해보고 선생님께 확인 받으세요. | |||
1) 213 → ? | |||
2) 99 → ? | |||
3) 194 → ? | |||
=== 4. 16진수 === | |||
'''10진수를 16진수로 변환'''하는 방법을 알아봅시다. | |||
16진수는 각 자리를 0~15로 표현할 수 있습니다. | |||
10진수를 16진수로 변환하기 위해서는 [10진수 → 2진수 → 16진수]로 단계별 과정을 거치면 쉽게 바꿀 수 있습니다. | |||
먼저 위에서 확인해보았던 10진수 [86]을 2진수로 변환하면 [1010110]입니다. 16진수는 2진수 자리를 4개씩 나눠 값을 변환하면 됩니다. | |||
[[파일:16진수.png|프레임없음|545x545픽셀]] | |||
10진수 [86]을 16진수로 변환하면 [56]입니다. | |||
만약, 10진수 [214]를 16진수로 변환하면 어떤 값이 나올까요? | |||
먼저 앞에서 배웠던 것을 이용해 10진수 [214]를 2진수로 변환하면 [11010110]라는 값이 나옵니다. | |||
2진수 값을 4개씩 나눠 16진수로 변환해봅시다. | |||
[[파일:16진수2.png|프레임없음|567x567픽셀]] | |||
4개씩 나눠 값을 변환하게되면 13, 6이라는 값이 나옵니다. | |||
그럼 10진수 [214]를 16진수로 변환한 결과는 [136]일까요? | |||
'''절대 아닙니다!''' | |||
값이 13/6을 나타낸 것인지 1/3/6을 나타낸 것인지 알 수 없습니다. | |||
16진수에서는 '''10~15까지의 값은 A~F까지의 알파벳'''으로 나타냅니다. | |||
{| class="wikitable" | |||
|+ | |||
!10진수 | |||
!16진수 | |||
|- | |||
|10 | |||
|A | |||
|- | |||
|11 | |||
|B | |||
|- | |||
|12 | |||
|C | |||
|- | |||
|13 | |||
|D | |||
|- | |||
|14 | |||
|E | |||
|- | |||
|15 | |||
|F | |||
|} | |||
따라서 10진수 [214]를 16진수로 표현하면 [D6]이 됩니다. | |||
==== ▶ 10진수 → 16진수 변환 퀴즈 ==== | |||
아래 3개의 문제를 직접 계산해보고 선생님께 확인 받으세요. | |||
1) 235 → ? | |||
2) 106 → ? | |||
3) 192 → ? | |||
=== 5. 비트연산자 === | |||
{| class="wikitable" | |||
!비트연산자 | |||
!설명 | |||
|- | |||
|& | |||
|AND | |||
|- | |||
|<nowiki>|</nowiki> | |||
|OR | |||
|- | |||
|^ | |||
|XOR | |||
|- | |||
|<< | |||
|LEFT SHIFT | |||
|- | |||
|>> | |||
|RIGHT SHIFT | |||
|} | |||
{| class="wikitable" | |||
|+&, |&, |, ^ | |||
!연산자 | |||
!비트 값1 | |||
!비트 값2 | |||
!결과 | |||
|- | |||
| rowspan="4" |& | |||
|1 | |||
|1 | |||
|1 | |||
|- | |||
|1 | |||
|0 | |||
|0 | |||
|- | |||
|0 | |||
|1 | |||
|0 | |||
|- | |||
|0 | |||
|0 | |||
|0 | |||
|- | |||
| rowspan="4" |<nowiki>|</nowiki> | |||
|1 | |||
|1 | |||
|1 | |||
|- | |||
|1 | |||
|0 | |||
|1 | |||
|- | |||
|0 | |||
|1 | |||
|1 | |||
|- | |||
|0 | |||
|0 | |||
|0 | |||
|- | |||
| rowspan="4" |^ | |||
|1 | |||
|1 | |||
|0 | |||
|- | |||
|1 | |||
|0 | |||
|1 | |||
|- | |||
|0 | |||
|1 | |||
|1 | |||
|- | |||
|0 | |||
|0 | |||
|0 | |||
|} | |||
[[파일:비트연산.png|프레임없음|633x633픽셀]] | |||
{| class="wikitable" | |||
|+<<, >> | |||
!연산자 | |||
!코드 | |||
!결과 | |||
!설명 | |||
|- | |||
| rowspan="3" |<< | |||
|101 << 2 | |||
|10100 | |||
| rowspan="3" |비트를 왼쪽으로 N번 이동 | |||
(0을 뒤에 N개 추가함) | |||
|- | |||
|1100 << 3 | |||
|1100000 | |||
|- | |||
|11 << 1 | |||
|110 | |||
|- | |||
| rowspan="3" |>> | |||
|101 >> 2 | |||
|1 | |||
| rowspan="3" |비트를 오른쪽으로 N번 이동 | |||
(맨 뒤 값 N개를 삭제함) | |||
|- | |||
|1101 >> 1 | |||
|110 | |||
|- | |||
|1100 >> 3 | |||
|1 | |||
|} | |||
[[파일:비트연산2.png|프레임없음|416x416픽셀]] | |||
헷갈린다면 <, > 모양에 따라 '''화살표'''를 그려보세요! | |||
화살표 방향으로 비트를 이동시키면 쉬워요! | |||
==== ▶ 비트 연산 퀴즈 ==== | |||
아래 문제를 직접 계산해보고 선생님께 확인 받으세요. | |||
아래 퀴즈의 결과를 10진수로 나타내보세요. | |||
1) 86 & 55 → ? | |||
2) 86 | 55 → ? | |||
3) 86 ^ 55 → ? | |||
4) 45 << 2 → ? | |||
5) 95 >> 3 → ? | |||
== 모듈 == | |||
=== 1. struct === | === 1. struct === | ||
C/C++ 구조를 파이썬에서 사용할 수 있도록 데이터 변환할 때 사용하는 모듈. | C/C++ 구조를 파이썬에서 사용할 수 있도록 데이터 변환할 때 사용하는 모듈. | ||
| 332번째 줄: | 764번째 줄: | ||
|? | |? | ||
|해당 패턴의 앞에 문자가 하나 있거나 없는 경우 | |해당 패턴의 앞에 문자가 하나 있거나 없는 경우 | ||
| | |\d? : 숫자가 하나 있거나 없어야 함 | ||
|- | |- | ||
|^ | |^ | ||
|이 패턴으로 | |이 패턴으로 시작해야 함 | ||
|^coders : coders로 시작해야 함(coders!, coders123 .. ) | |^coders : coders로 시작해야 함(coders!, coders123 .. ) | ||
|- | |- | ||
| 347번째 줄: | 779번째 줄: | ||
|- | |- | ||
|[문자열] | |[문자열] | ||
|[문자열]에 있는 문자가 포함된 | |[문자열]에 있는 문자가 포함된 문자여야 함. | ||
|["CcOoders"] : Coders, COd | |["CcOoders"] : Coders, COd | ||
|- | |- | ||
|[^문자열] | |[^문자열] | ||
|[문자열]과 반대로 피해야할 문자열의 집합. [^문자열]에 있는 문자열을 제외한 | |[문자열]과 반대로 피해야할 문자열의 집합. [^문자열]에 있는 문자열을 제외한 문자여야 함. | ||
|["^ABC"] : coders, Python | |["^ABC"] : coders, Python | ||
|- | |- | ||
|<nowiki>|</nowiki> | |<nowiki>|</nowiki> | ||
|두 패턴 중 | |두 패턴 중 하나여야 함 | ||
|<nowiki>a | b : a 또는 b 이어야 함</nowiki> | |<nowiki>a | b : a 또는 b 이어야 함</nowiki> | ||
|- | |- | ||
| 364번째 줄: | 796번째 줄: | ||
|{n,m} | |{n,m} | ||
|앞 패턴이 n 이상 m 이하로 반복 | |앞 패턴이 n 이상 m 이하로 반복 | ||
|\d{1,3} : 숫자가 1개 이상 3개 이하로 | |\d{1,3} : 숫자가 1개 이상 3개 이하로 있어야 함 | ||
|- | |- | ||
|$ | |$ | ||
|이 패턴으로 | |이 패턴으로 종료되야 함. | ||
|coders$ : coders로 | |coders$ : coders로 종료되어야 함 (abc!coders, 2024coders) | ||
|- | |- | ||
|\d | |\d | ||
2024년 10월 7일 (월) 18:07 기준 최신판
진법 (2진법, 8진법, 16진법), 비트 연산자
N진법 ?
N진법이란 0~N-1로 각 자리를 표현해 나타내는 수 입니다.
일반적으로 우리가 사용하는 숫자는 10진수입니다. 각 자리를 0~9로 나타내기 때문에 10진수이죠!
0~9 의 수로 숫자를 나타내다가 더이상 표현할 수 없을 때 한 자리를 높여 다음 자리를 표현합니다.
예를 들어, 38 + 75를 그림으로 알아봅시다.
일의 자리를 먼저 더한 결과를 생각해보면 13입니다. 10진수는 각 자리에 0~9까지만 나타낼 수 있으므로 1을 십의 자리로 올려 계산합니다.
다음 10의 자리를 계산해봅시다. 3과 8을 더한 결과는 10입니다. 일의 자리에서 올라온 1과 함께 계산하면 11입니다. 10진수는 각 자리에 0~9까지만 나타낼 수 있으므로 백의 자리로 1을 올려 계산합니다.
우리가 항상 더하기 한 결과를 위와 같은 과정으로 나타내 보았습니다.
▶ 2진수 더하기 계산 방법
그럼 2진수 더하기를 한 번 예시를 통해 확인해봅시다.
2진수는 각 자리를 0~1로 표현할 수 있습니다. 합한 결과가 2가 되면 다음 자리로 1을 올림하여 계산하면 됩니다.
예를 들어, 101 + 111를 그림으로 알아봅시다.
먼저 10진수처럼 맨 뒤 자리부터 계산합니다.
1 + 1 은 2입니다. 2진수는 각 자리를 0~1로 나타낼 수 있기 때문에 1을 다음 자리로 올려 계산합니다.
다음 자리를 계산해봅시다. 0과 1을 더한 값과 넘어온 1을 함께 계산하면 2입니다. 2진수는 각 자리를 0~1로 나타낼 수 있기 때문에 1을 다음 자리로 올려 계산합니다.
다음 자리를 계산해봅시다. 1과 1을 더한 값과 넘어온 1을 함께 계산하면 3입니다. 2진수는 각 자리를 0~1로 나타낼 수 있기 때문에 1을 다음 자리로 올려 계산합니다.
이진수 101 + 111 의 결과는 1100입니다. 숫자가 0과 1만 존재하는 수라고 생각해보면 쉬워요!
▶ 2진수 더하기 퀴즈
아래 3개의 문제를 직접 계산해보고 선생님께 확인 받으세요.
1) 1110 + 101 = ?
2) 10101 + 1101 = ?
3) 1011 + 1101 = ?
1. 2진수
위에서 간단히 2진수에 대해서 확인해보았습니다.
2진수는 0~1로 이루어진 수 입니다.
2진수의 값을 나타내는 방법에 대해서 배워봅시다.
먼저 너무나도 당연하게 사용하는 10진수를 생각해봅시다.
[19803] 라는 수가 있다면 이 수를 나타내는 방법은 아래와 같습니다.
10진수는 위의 표처럼 나타내고 사용합니다.
1 X 10000 + 9 X 1000 + 8 X 100 + 0 X 10 + 3 X 1
10진수와 2진수는 각 자리를 나타내는 수의 크기가 다를 뿐 개념은 같습니다.
[101011] 라는 수는 어떻게 표현할까요?
2진수를 나타내는 방법을 표로 나타내면 아래와 같습니다.
10진수와 마찬가지로 위의 표처럼 나타내고 사용합니다.
1 X 32 + 0 X 16 + 1 X 8 + 0 X 4 + 1 X 2 + 1 X 1
따라서 [101011]라는 이진수를 십진수로 나타내면 위의 계산을 통해 [43]라는 것을 알 수 있습니다.
2. 10진수 → 2진수 변환하기
2진수에 대해서 알아보았습니다. 그럼 10진수 N이라는 값을 2진수로 변환하는 방법을 알아봅시다.
1) 2진수 변환 방법① : 2진수 자리를 이용해 채우기
위에서 배운 것을 이용해 각 자리를 생성하고 10진수의 값을 차례로 값을 넣어보면 됩니다.
10진수 [86]을 2진수로 나타내봅시다.
86를 2진수로 변환하기 위해서 2진수 표를 만들어봅시다.
가장 큰 자리 수부터 채우면 됩니다.
현재 만든 표에서는 가장 큰 수가 128입니다. 그러나 86은 128보다 작아서 128자리는 0으로 채우고 넘어갑니다.
다음은 64자리 입니다. 64자리를 1로 채웁니다.
남은 값 [22]를 이용해 다음 자리를 계산합니다.
다음 자리는 32입니다. 22는 32보다 작아서 32자리는 0으로 채우고 넘어갑니다.
다음은 16자리 입니다. 16자리를 1로 채웁니다.
남은 값 [6]을 이용해 다음 자리를 계산합니다.
다음 자리는 8입니다. 6은 8보다 작아서 8자리는 0으로 채우고 넘어갑니다.
다음은 4자리 입니다. 4자리를 1로 채웁니다.
남은 값 [2]를 이용해 다음 자리를 계산합니다.
2자리를 1로 채웁니다. 남은 값은 0이므로 나머지 칸을 모두 0으로 채웁니다.
결과적으로 10진수 [86]을 2진수로 변환하면 [1010110]입니다.
2) 2진수 변환 방법② : 2로 나눈 몫과 나머지를 이용해 변환하기
두 번째 방법은 10진수 값을 2로 나눈 몫과 나머지를 계산하여 2진수로 변환하는 방법입니다.
이 방법이 더 쉬울 수 있어요!
위의 예제처럼 [86]을 2진수로 변환하는 과정을 아래 그림으로 알아봅시다.
아래 그림처럼 86을 계속 2로 나눠봅시다. 몫이 1이될 때까지 몫과 나머지를 작성합니다.
몫이 1이 되는 경우까지 작성 후 주황선을 따라 순서대로 값을 적어주면 10진수 값을 2진수로 변환한 값입니다.
따라서 10진수 [86]을 2진수로 변환하면 [1010110]입니다.
위에서 2진수의 자리를 채워 변환하는 방법과 같은 값이 나오는 것을 확인할 수 있습니다.
▶ 10진수 → 2진수 변환 퀴즈
아래 3개의 문제를 직접 계산해보고 선생님께 확인 받으세요.
1) 57 → ?
2) 19 → ?
3) 156 → ?
▶ 2진수 → 10진수 변환 퀴즈
아래 3개의 문제를 직접 계산해보고 선생님께 확인 받으세요.
1) 1000100 → ?
2) 11111 → ?
3) 101101 → ?
3. 8진수
10진수와 2진수에 대해 공부해보았습니다.
그럼 이번엔 8진수에 대해서 배워봅시다.
앞에서 배웠듯 10진수는 각 자리를 0~9까지 나타낼 수 있고 2진수는 0~1까지 나타낼 수 있습니다.
그러므로 8진수는 0~7까지 나타낼 수 있답니다!
그럼 10진수를 8진수로 변환하는 방법을 알아봅시다.
10진수를 8진수로 변환하기 위해서는 [10진수 → 2진수 → 8진수]로 단계별 과정을 거치면 쉽게 바꿀 수 있습니다.
먼저 위에서 확인해보았던 10진수 [86]을 2진수로 변환하면 [1010110]입니다. 8진수는 2진수 자리를 3개씩 나눠 값을 변환하면 됩니다.
2진수를 맨 뒷 자리부터 3개씩 나눠봅시다.
맨 앞의 1은 앞에 2개의 값이 없습니다. 이때는 앞에 2개의 0이 있다고 생각해보세요.
그리고 각 자리의 값을 8진수로 변환하게 되면 아래와 같습니다.
2진수를 8진수로 변환하면 [126]이 됩니다.
▶ 10진수 → 8진수 변환 퀴즈
아래 3개의 문제를 직접 계산해보고 선생님께 확인 받으세요.
1) 213 → ?
2) 99 → ?
3) 194 → ?
4. 16진수
10진수를 16진수로 변환하는 방법을 알아봅시다.
16진수는 각 자리를 0~15로 표현할 수 있습니다.
10진수를 16진수로 변환하기 위해서는 [10진수 → 2진수 → 16진수]로 단계별 과정을 거치면 쉽게 바꿀 수 있습니다.
먼저 위에서 확인해보았던 10진수 [86]을 2진수로 변환하면 [1010110]입니다. 16진수는 2진수 자리를 4개씩 나눠 값을 변환하면 됩니다.
10진수 [86]을 16진수로 변환하면 [56]입니다.
만약, 10진수 [214]를 16진수로 변환하면 어떤 값이 나올까요?
먼저 앞에서 배웠던 것을 이용해 10진수 [214]를 2진수로 변환하면 [11010110]라는 값이 나옵니다.
2진수 값을 4개씩 나눠 16진수로 변환해봅시다.
4개씩 나눠 값을 변환하게되면 13, 6이라는 값이 나옵니다.
그럼 10진수 [214]를 16진수로 변환한 결과는 [136]일까요?
절대 아닙니다!
값이 13/6을 나타낸 것인지 1/3/6을 나타낸 것인지 알 수 없습니다.
16진수에서는 10~15까지의 값은 A~F까지의 알파벳으로 나타냅니다.
| 10진수 | 16진수 |
|---|---|
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
따라서 10진수 [214]를 16진수로 표현하면 [D6]이 됩니다.
▶ 10진수 → 16진수 변환 퀴즈
아래 3개의 문제를 직접 계산해보고 선생님께 확인 받으세요.
1) 235 → ?
2) 106 → ?
3) 192 → ?
5. 비트연산자
| 비트연산자 | 설명 |
|---|---|
| & | AND |
| | | OR |
| ^ | XOR |
| << | LEFT SHIFT |
| >> | RIGHT SHIFT |
| 연산자 | 비트 값1 | 비트 값2 | 결과 |
|---|---|---|---|
| & | 1 | 1 | 1 |
| 1 | 0 | 0 | |
| 0 | 1 | 0 | |
| 0 | 0 | 0 | |
| | | 1 | 1 | 1 |
| 1 | 0 | 1 | |
| 0 | 1 | 1 | |
| 0 | 0 | 0 | |
| ^ | 1 | 1 | 0 |
| 1 | 0 | 1 | |
| 0 | 1 | 1 | |
| 0 | 0 | 0 |
| 연산자 | 코드 | 결과 | 설명 |
|---|---|---|---|
| << | 101 << 2 | 10100 | 비트를 왼쪽으로 N번 이동
(0을 뒤에 N개 추가함) |
| 1100 << 3 | 1100000 | ||
| 11 << 1 | 110 | ||
| >> | 101 >> 2 | 1 | 비트를 오른쪽으로 N번 이동
(맨 뒤 값 N개를 삭제함) |
| 1101 >> 1 | 110 | ||
| 1100 >> 3 | 1 |
헷갈린다면 <, > 모양에 따라 화살표를 그려보세요!
화살표 방향으로 비트를 이동시키면 쉬워요!
▶ 비트 연산 퀴즈
아래 문제를 직접 계산해보고 선생님께 확인 받으세요.
아래 퀴즈의 결과를 10진수로 나타내보세요.
1) 86 & 55 → ?
2) 86 | 55 → ?
3) 86 ^ 55 → ?
4) 45 << 2 → ?
5) 95 >> 3 → ?
모듈
1. struct
C/C++ 구조를 파이썬에서 사용할 수 있도록 데이터 변환할 때 사용하는 모듈.
1) pack : 원하는 값들을 특정 포맷으로 하나의 객체로 합쳐줌
2) unpack : 합쳐진 객체를 특정 포맷으로 여러 객체로 분리해줌
2. datetime
날짜와 시간을 다루는 모듈.
1) datetime 클래스 : 년, 월, 일, 시간, 분, 초, 마이크로초 등을 포함한 객체 생성
import datetime
now = datetime.datetime.now()
print(now)
# 출력 결과
# 2024-09-14 01:55:57.531073
2) strptime : 문자열을 datetime 객체로 변환
import datetime
s = "2024-09-14 11:20:45"
date = datetime.datetime.strptime(s, "%Y-%m-%d %H:%M:%S")
print(date)
# 출력 결과
# 2024-09-14 11:20:45
3) strftime : datetime 객체를 지정한 포맷에 맞게 문자열로 변환
import datetime
now = datetime.datetime.now()
date1 = now.strftime("%Y년 %m월 %d일 %H:%M:%S")
print(date1)
# 출력 결과
# 2024년 09월 14일 02:08:51
date2 = now.strftime("%m월 %d일 !! ")
print(date2)
# 출력 결과
# 09월 14일 !!
date3 = now.strftime("%Y.%m.%d. %H시 %M분 %S초")
print(date3)
# 출력 결과
# 2024.09.14. 02시 10분 29초
4) 포맷
| 포맷코드 | 설명 | 예 |
|---|---|---|
| %a | 요일 줄임말 | Sun, Mon, ..., Sat |
| %A | 요일 | Sunday, Monday, ..., Saturday |
| %w | 요일을 숫자로 표시 (일요일:0, 월요일:1, ..., 토요일:6) | 0, 1, ..., 6 |
| %d | 일 | 01, 02, ..., 31 |
| %b | 월 줄임말 | Jan, Feb, ..., Dec |
| %B | 월 | January, February, ..., December |
| %m | 숫자 월 | 01, 02, ..., 12 |
| %y | 두 자릿수 연도 | 01, 02, ..., 99 |
| %Y | 네 자릿수 연도 | 0001, 0002, ..., 2023, 2024, ..., 9999 |
| %H | 시간(24시간) | 00, 01, ..., 23 |
| %I | 시간(12시간) | 01, 02, ..., 12 |
| %p | AM, PM | AM, PM |
| %M | 분 | 00, 01, ..., 59 |
| %S | 초 | 00, 01, ..., 59 |
| %Z | 시간대 | 대학민국 표준시 (비어 있음), UTC, EST, CST |
| %j | 1월 1일부터 경과한 일수 | 001, 002, ..., 366 |
| %U | 1년중 주차, 일요일이 한 주의 시작으로 | 00, 01, ..., 53 |
| %W | 1년중 주차, 월요일중 주차, 월요일 | 00, 01, ..., 53 |
| %c | 날짜, 요일, 시간을 출력, 현재 시간대 기준 | Sat Sep 14 02:19:16 2024 |
| %x | 날짜를 출력, 현재 시간대 기준 | 09/14/24 |
| %X | 시간을 출력, 현재 시간대 기준 | 02:20:13 |
3. calendar
1) calendar : 입력한 년도의 달력을 출력
import calendar
print(calendar.calendar(2024))
[출력 결과]
2) month : 입력한 년도의 원하는 월 출력
import calendar
print(calendar.month(2024, 10))
[출력 결과]
4. math
1) round : 지정한 소수점 자릿수에 맞춰 반올림하는 함수
import math
a=7.147
print(round(a))
print(round(a,-1))
print(round(a,1))
print(round(a,2))
print(round(a,3))
print(round(a,4))
# 출력 결과
# 7
# 10.0
# 7.1
# 7.15
# 7.147
# 7.147
2) ceil : 실수를 올림하여 정수로 반환
import math
a=7.147
print(math.ceil(a))
b=3.7
print(math.ceil(b))
# 출력 결과
# 8
# 4
3) floor : 실수를 내림하여 정수로 반환
import math
a=7.147
print(math.floor(a))
b=3.7
print(math.floor(b))
# 출력 결과
# 7
# 3
4) factorial : 1~N까지 곱한 값 반환 (N! : 팩토리얼)
import math
a=5
print(math.factorial(a))
b=3
print(math.factorial(b))
# 출력 결과
# 120
# 6
5) gnd(a, b) : a와 b의 최대공약수 반환
import math
a = 20
b = 24
print(math.gcd(a,b))
# 출력 결과
# 4
6) sqrt : 제곱근 반환
import math
a = 4
b = 121
c = 25
print(math.sqrt(a))
print(math.sqrt(b))
print(math.sqrt(c))
# 출력 결과
# 2.0
# 11.0
# 5.0
7) pow(a, b) : a의 b제곱 값 반환
import math
print(math.pow(2,3))
print(math.pow(2,5))
print(math.pow(3,2))
# 출력 결과
# 8.0
# 32.0
# 9.0
5. random
1) random : 0 이상 1 미만의 무작위 값 반환
import random
print(random.random())
print(random.random())
print(random.random())
print(random.random())
print(random.random())
# 출력 결과
# 0.789151304563551
# 0.377096725708465
# 0.4463789421422576
# 0.03214667403259963
# 0.704154756663026
2) randint(a, b) : a 이상 b 이하의 정수 중 무작위 값 반환
import random
print(random.randint(1,5))
print(random.randint(1,5))
print(random.randint(1,5))
print(random.randint(1,5))
print(random.randint(1,5))
# 출력 결과
# 1
# 3
# 5
# 3
# 5
3) choice : 무작위 원소를 뽑아 반환
import random
arr = [10, 2, 56, 3, 99]
print(random.choice(arr))
print(random.choice(arr))
print(random.choice(arr))
# 출력 결과
# 3
# 10
# 99
4) shuffle : 요소를 무작위로 섞어 반환
import random
arr = [10, 2, 56, 3, 99]
random.shuffle(arr)
print(arr)
random.shuffle(arr)
print(arr)
# 출력 결과
# [99, 10, 3, 56, 2]
# [10, 56, 99, 3, 2]
5) sample : 지정한 개수만큼 임의로 요소를 선택하여 반환
import random
arr = [10, 2, 56, 3, 99]
print(random.sample(arr, 2))
print(random.sample(arr, 3))
# 출력 결과
# [10, 56]
# [56, 99, 2]
6. pickle
파이썬에서 사용하는 다양한 자료를 객체 그대로 파일로 저장하고 이를 불러올 때 사용하는 모듈.
7. os
1) mkdir : 새로운 디렉토리 생성
2) getpid : 현재 프로세스 ID를 반환
3) setregid : 현재 프로세스의 그룹 ID를 설정
4) read : 파일 읽기
5) chdir : 디렉토리의 위치 변경
6) getcwd : 현재 작업 중인 파일의 경로 반환
7) listdir : 해당 경로에 위치하는 파일과 디렉토리 반환
8) removedirs : 해당 경로의 디렉토리 삭제
9) rename : 파일 이름 변경
8. traceback
1) format : 오류가 발생한 위치의 추석 결과를 반환
9. re
정규표현식을 사용할 수 있는 모듈
| 정규표현식 | 설명 | 예제 |
|---|---|---|
| . | 임의의 문자 하나 | a.c : a와 c 사이 임의의 문자가 있음. (abc, adc ..) |
| ? | 해당 패턴의 앞에 문자가 하나 있거나 없는 경우 | \d? : 숫자가 하나 있거나 없어야 함 |
| ^ | 이 패턴으로 시작해야 함 | ^coders : coders로 시작해야 함(coders!, coders123 .. ) |
| + | 앞 패턴이 하나 이상 | \d+coders : coders 앞에 숫자가 하나 이상 |
| * | 앞 패턴이 0개 이상 | \d*coders : coders 앞에 숫자가 0개 이상 |
| [문자열] | [문자열]에 있는 문자가 포함된 문자여야 함. | ["CcOoders"] : Coders, COd |
| [^문자열] | [문자열]과 반대로 피해야할 문자열의 집합. [^문자열]에 있는 문자열을 제외한 문자여야 함. | ["^ABC"] : coders, Python |
| | | 두 패턴 중 하나여야 함 | a | b : a 또는 b 이어야 함 |
| {n} | 앞 패턴을 n번 반복 | \d{5} : 숫자가 5개 있어야함 |
| {n,m} | 앞 패턴이 n 이상 m 이하로 반복 | \d{1,3} : 숫자가 1개 이상 3개 이하로 있어야 함 |
| $ | 이 패턴으로 종료되야 함. | coders$ : coders로 종료되어야 함 (abc!coders, 2024coders) |
| \d | 숫자 0~9 | \d : 0~9 숫자 |
| \w | 숫자나 알파벳(문자를 의미) | \w : 문자 1개 (a, b, 1 .. ) |
| \n | 줄 바꿈 | 엔터 |
1) compile : 정규표현식 패턴을 정하는 함수
2) match : 문자열의 처음이 정규표현식과 매치되는지 확인 (접두사가 패턴과 일치하는지 판단)
3) fullmatch : 문자열 전체가 해당 패턴인지 확인
import re
pattern = re.compile('o[gh]')
print(pattern.match('oh'))
print(pattern.fullmatch('oh'))
# 출력 결과
# <re.Match object; span=(0, 2), match='oh'>
# <re.Match object; span=(0, 2), match='oh'>
print(pattern.match('oha'))
print(pattern.fullmatch('oha'))
# 출력 결과
# <re.Match object; span=(0, 2), match='oh'>
# None
import re
pattern = re.compile('...[abc]*')
print(pattern.match('321ca'))
print(pattern.fullmatch('321ca'))
# 출력 결과
# <re.Match object; span=(0, 5), match='321ca'>
# <re.Match object; span=(0, 5), match='321ca'>
print(pattern.match('321coders'))
print(pattern.fullmatch('321coders'))
# 출력 결과
# <re.Match object; span=(0, 4), match='321c'>
# None